- 강의 영상
-Linear classifier
강의에서는 Linear classifier를 통하여 현재 W가 좋은지, 구린지를 Loss function을 통해 정량적으로 수치화 시켜주는 방법을 소개하고, 이 때의 Loss function을 최소화 하는 W를 찾는 과정을 optimzation 과정이라 정의한다.

강의에서 정의한 Linear classifier는 들어온 입력 이미지 32*32*3 픽셀 크기의 이미지 벡터를 하나의 긴 벡터로 펼치고. 가중치 W벡터를 곱하여 최종 10개의 class score에 대한 값을 출력한다. 예시에서는 좀 더 simple한 상황을 고려하여 다음과 같이 3개의 class로 줄여서 예시를 든다. 위의 예시에서는 Loss function으로 "Hinge loss"를 사용하였다. 오른쪽 아래의 Hinge loss 수식에서 sj는 Linear classifier로 부터 나온 j번째 카테고리의 출력 score 점수를 의미하고 syi는 해당 사진의 정답 score 점수를 의미한다. 예시에서 safe margin은 1로 설정하였다. (safe margin의 크기는 크게 중요하지 않음.)
Hinge Loss의 특징을 간단하게 살펴보면, 실제 정답 score값이 커질수록 loss값이 줄어드는 것을 그래프를 통해 확인할 수 있다. 이때 해당 그래프의 y축은 loss 값을 x축은 실제 정답 score값임을 알 수 있다.

해당 Loss function 수식을 통해 실제 loss를 계산하는 과정을 보여준다. 3번째 사진의 정답 레이블은 frog이므로 frog를 제외한 score를 돌면서, 해당 score에 frog score(정답 레이블 score)를 빼고 safe margin을 더한 값과 0을 비교하여 모두 더해준다.

위와 같이 각 카테고리 Loss값을 모두 더하여 평균을 내면 해당 모델에서의 최종 Loss 값이 된다.

해당 모델을 처음 학습시키는 상황이라면, 일반적으로 행렬W를 임의의 작은 수로 초기화 시키게 되고, 그렇게 하면 처음 학습시 결과 스코어 값은 0에 가까운 임의의 일정한 값들이 나오게 된다. score 값들이 0에 가깝고 값이 서로 비슷하기 때문에 Multiclass SVM에서의 Loss는 (The number of class - 1)이 될것이라고 예상할 수 있다. 이러한 성질을 디버깅하는데 이용할 수 있다는 것이 강의에서의 설명이었다.

해당 내용은 우리가 학습을 통해 Loss가 0이 되는 W값을 찾았다면, 그 W 값이 unique한가? 라는 질문이다. 정답은 unique하지 않다는 것이고, 반례를 쉽게 찾을 수 있다. Loss가 0인 W 행렬 전체에 scalar 2를 곱하게 되면, score 값도 2배씩 증가하게 되고 Hinge Loss의 margin을 계산해도 여전히 0보다 작은 값이 나오기 때문에 똑같이 Loss는 0을 가질 것이라고 예상할 수 있었다.

다음의 예시를 통해 Loss가 0인 W에 대해서 2W일 경우의 실제 계산한 결과를 볼 수 있다.
-L1, L2 Regularization
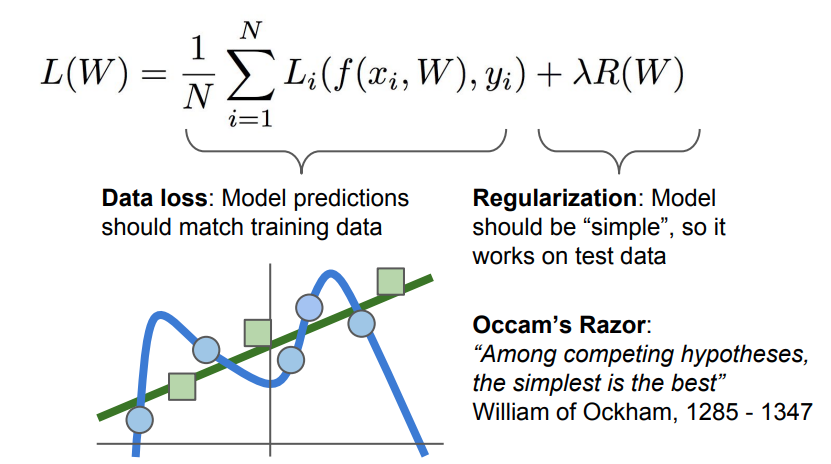
우리가 Loss를 찾는 과정에서 중요하게 생각해야 할것은 training data에 대한 loss가 아니라 test data에 대한 loss이다. 따라서 학습과정에서의 Loss가 0인것을 선택하는 것은 모순적일 수 있다. 위의 그림에서 파란색점의 training data와 초로색점의 test 데이터가 있을때, 트레이닝 데이터에 W가 너무 fit하게 된다면, 우리는 실제로 초록색 선을 찾고 있지만, 파란색 선과 같은 결과가 나올수 있다. 이러한 현상을 overfiting이라고 하며, 이러한 overfiting을 해결하는 방법을 통틀어서 Regularization이라 한다.
위의 Loss식을 나타내는 L(W)에서 +하기를 기준으로 왼쪽의 항은 Data의 loss값을 나타내고, 오른쪽 항은 Regularization loss를 나타낸다. Regularization loss term을 이용하여 우리가 구하고자 하는 모델이 저차 다항식을 선호하도록 유도하는 것이다.

Regularization에 대한 식은 여러 종류가 있다. 여기서는 L2,L1 regularization term에 대해 살펴본다. 보편적인 regularization은 weight decay라고 불리는 L2 regularization이다. 위의 term을 통해 모델이 트레이닝 데이터셋에 완전히 핏하지 못하도록 모델의 복잡도에 대해 패널티를 부여한다. 이때, 빨간 박스의 R(W) 앞 람다는 하이퍼 파라미터이다.

L2와 L1 Regularization의 차이에 대한 issue를 설명한다. Linear classification 관점에서는 w1과 w2 모두 x와의 내적결과가 1로 동일하지만, L2 regularization은 w2더 선호한다.(L2 norm의 크기가 더 작기 때문) 즉, L2는 x의 모든 요소가 영향을 줬으면 하는 바람의 관점으로 볼 수 있다. 따라서 변동이 심한 어떤 입력 x가 있으면 x의 특정 요소에만 의존하기보다 모든 x의 요소가 골고루 영향을 미치기 원할때 L2를 사용한다.(좀 더 Robust한 x를 선호)
강의에서는 L1은 sparse한 solution(0이 아닌 요소들의 갯수로 complexity를 측정)을 선호하고, L2는 W의 요소가 전체적으로 퍼졌을 때 덜 복작하다고 정리한다.
-Softmax Classifier

강의에서 스코어에 추가적인 의미를 부여하기 위해서 softmax라는 함수를 사용한다. softmax 함수는 위의 P(Y=k l X=xi)의 식을 통해 구한다. 해당 함수를 사용하여 스코어의 클레스별 확률분포를 알 수 있다. 해당 softmax의 출력값은 0~1 사이의 값이므로 해당 함수의 Loss는 1일때 최소, 0일 때 최대가 되어야 한다. 따라서 Loss function으로 softmax function에 -log를 취해준다.

위의 슬라이드는 앞에서의 3개 카테고리를 분류하는 task에 softmax function을 적용한 것이다. 녹색 박스에서 알 수 있듯이 softmax는 score를 normalize하여 probabilities가 출력 되는것을 알 수 있다. (보라색은 최종 Loss 값이다.)
강의에서는 softmax를 이용한 디버깅 전략 하나를 소개한다. 초기 initialization 과정에서 s값이 0근처에 모여있는 아주작은 숫자를 생각해보자. 예를들면 필자는 위의 세개의 카테고리 score가 극단적으로 0과 아주가까워서 모두 0이라고 가정을 한다. 그러면 exp 연산을 하면 0승이 되므로 세 score의 빨간 박스의 값이 모두 1이 나올것이다. (실제로는 1과 아주가까운 값) 그러면 softmax의 수식에 의해 분모는 class의 갯수만큼의 1을 더한 값, 분자는 1이 된다. 즉 -log(1/C)가 되는것이다. log 성질을 이용하면 logC임을 알 수있고, 이를 디버깅 전략으로 사용할 수 있다.
-Optimization
지금까지 딥러닝에 사용하는 Linear classfication의 함수 f, 이를 평가하는 Loss function, 모델이 복잡해지는 것을 막는 Regularization term에 대해 알아보았다. 이제는 해당 과정에서 Loss function의 값이 최소가 되는 W를 어떻게 찾아나갈 것인지에 대한 Optimization 과정에 대해 알아본다.

강의에서 사용하는 전략은 지역적인 기하학적 특성을 이용하는 것이다. 우리는 위와같이 1차원 공간에서의 도함수를 알고 있다. 실제에서는 x는 scalar가 아닌 vector이므로 다변수에 대해 일반화 시키면 우리가 원하는 Gradient는 벡터 x에 대한 각 요소의 편도함수들이 될것이다. 이는 해당 방향에 대한 기울기 정보를 나타낸다. gradient 방향이 해당함수에서 가장 많이 올라가는 방향이라는 성질을 이용하여, 반대 방향으로 업데이트시킨다. 그렇다면 해당함수에서 가장 많이 내려가는 방향이 될 것이다. 우리는 계산한 gradient를 가지고 파라미터 벡터를 반복적으로 업데이트하는데 사용한다.

컴퓨터는 "유한 차분법"을 이용하여 목표하는 gradient를 계산한다. 위에서는 앞의 예제에서 loss 1.25347을 갖는 W를 가져왔다. 해당 idea는 간단하다. 우리가 원하는 gradient dW를 구하기 위해 유한 차분법을 이용한다. 이때 아주 작은 스텝 h를 이용한다. (여기서는 0.0001) 그렇게 w값과 h값을 대입하여 값을 구해준것이 가장 오른쪽의 gradient dW 값이다.
하지만 이와 같은 방법은 함수 f가 CNN같이 큰 함수이거나, 깊은 신경망에서 W 파라미터 갯수가 엄청 많아지면 엄청나게 비효율적이고 시간이 오래걸리는 방법이 된다. 그래서 강의에서는 새로운 idea를 제시한다.


앞에서와 같은 비효율을 줄이기 위해서 우리는 미분을 이용한다. (수치적으로 푸는것이 아닌 해석적 풀이) 앞에서와 같이 W를 모두 순회하는 것이 아니라 gradient를 나타내는 수식을 찾아내서 한번에 gradient dW를 계산한다. 이러한 계산과정은 lecture 4에서 살펴볼 수 있다.
[강의정리] Lecture 4: Backpropagation and Neural Networks
-강의 영상 - Introduction 이전 강의인 Lecture 3에서는 Loss function에서의 Loss값의 gradient를 이용해서 가중치를 업데이트하는 optimization 과정을 살펴봤다. Lecture 4에서는 Optimization 과정에서 가중..
gbjeong96.tistory.com
출처 : Stanford University School of Engineering, http://cs231n.stanford.edu/
'AI > cs231n' 카테고리의 다른 글
| [강의정리] Lecture 7: Training Neural Networks, Part 2 (0) | 2022.03.28 |
|---|---|
| [강의정리] Lecture 6: Training Neural Networks, Part 1 (0) | 2021.12.24 |
| [강의정리] Lecture 5: Convolutional Neural Networks (0) | 2021.09.24 |
| [강의정리] Lecture 4: Backpropagation and Neural Networks (2) | 2021.09.13 |
| [강의정리] Lecture 2: Image Classification pipeline (0) | 2021.08.29 |



